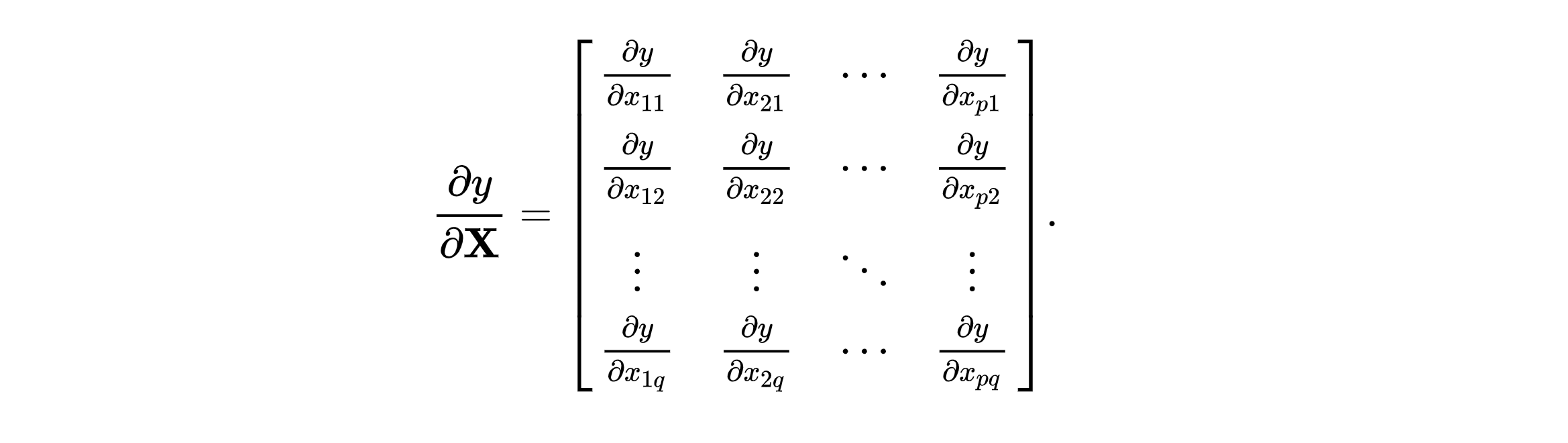在信号处理的公式推导中难免会遇到复数矩阵的求导问题，我自己也在 beamforming 相关的工作中两度接触复数矩阵求导，但过一段时间之后就很容易忘掉求导的一些规则，以致于想要再次尝试时不得不重新学习一遍。

所以，写下这篇文章的目的也就是记录下复数矩阵求导所需要的一些关键知识，以便忘掉之后能快速上手。

本文主要根据文献 [R1] 中给出的复数导数定义和推导方式来进行梳理，并对文章内容进行了适当地补充和调整。

文献 [R1] 中介绍的复偏导定义实际上有一个更广为人知的名称，即 Wirtinger derivatives（详见 [R2]），但不知为何 [R1] 没有引用任何相关文献和提及这一名称。

复标量函数关于复标量/复向量的偏导数

基本定义

首先从最简单的情况——复标量的偏导数开始。

定理一

令 $g: \mathbb{C} \times \mathbb{C} \mapsto \mathbb{C}$ 是复数 $z$ 及其共轭 $z^*$ 的一个函数，并且 $g$ 分别关于 $z$ 和 $z^*$ 都是独立的解析函数^{[1][2][3][4][5]}。令 $f: \mathbb{R} \times \mathbb{R} \mapsto \mathbb{C}$ 是关于实变量 $x$ 和 $y$ 的函数，且满足 $g(z, z^*) = f(x,y)$，其中 $z=x+iy$。那么：
偏导数 $\partial g / \partial z$（将 $g$ 函数中的 $z^*$ 看作常数）等价于 $\dfrac{1}{2}\left(\dfrac{\partial f}{\partial x} - i \dfrac{\partial f}{\partial y}\right)$。
类似地，$\partial g / \partial z^*$ 等价于 $\dfrac{1}{2}\left(\dfrac{\partial f}{\partial x} + i \dfrac{\partial f}{\partial y}\right)$。

〖展开以查看证明〗

首先考虑一个更一般的情况，令 $g: \mathbb{C} \times \mathbb{C} \mapsto \mathbb{C}$ 是两个复变量 $z_1$ 和 $z_2$ 的函数，其中 $z_1$ 和 $z_2$ 分别都是两个实变量 $x$ 和 $y$ 的函数 $(\mathbb{R} \times \mathbb{R} \mapsto \mathbb{C})$：

$\quad\left.\begin{aligned}z_1 &= x+ky\\z_2 &= x-ky\end{aligned}\ \right\} \hspace{15em}(1)$
$\quad x, y \in \mathbb{R}$
$\quad z_1, z_2, k \in \mathbb{C} \qquad\qquad k \neq 0$
其中 $k$ 是任意非零的复常数。

如果 $g$ 分别关于 $z_1$ 和 $z_2$ 都是独立的解析函数，我们可以定义两个解析函数^[6]$g_{1a}$ 和 $g_{2b} (\mathbb{C} \mapsto \mathbb{C})$ 使得 $g_{1a}(z) = g(z, a)$ 以及 $g_{2b}(z) = g(b, z)$ 对所有 $a, b \in \mathbb{C}$ 成立。
如此，我们可以用普通复微分的形式来定义 $g$ 的偏导数，从而说明偏导数是存在的：

$\quad\dfrac{\partial g}{\partial z_1}(z_1, z_2) = \dfrac{\operatorname{d}\!g_{1 z_2}}{\operatorname{d}\!z_1}(z_1)$

$\quad\dfrac{\partial g}{\partial z_2}(z_1, z_2) = \dfrac{\operatorname{d}\!g_{2 z_1}}{\operatorname{d}\!z_2}(z_2)$

又根据条件

$\quad g(z_1, z_2) = f(x, y) \hspace{13.5em}(2)$

分别对 $x$ 和 $y$ 取偏导，并利用链式法则，可以得到

$\quad\left.\begin{aligned}\dfrac{\partial g}{\partial z_1} \dfrac{\partial z_1}{\partial x} + \dfrac{\partial g}{\partial z_2} \dfrac{\partial z_2}{\partial x} &= \dfrac{\partial f}{\partial x}\\\\\dfrac{\partial g}{\partial z_1} \dfrac{\partial z_1}{\partial y} + \dfrac{\partial g}{\partial z_2} \dfrac{\partial z_2}{\partial y} &= \dfrac{\partial f}{\partial y}\end{aligned}\ \right\} \hspace{8.5em}(3)$

从公式 (1) 中我们可以得到

$\quad\dfrac{\partial z_1}{\partial x} = \dfrac{\partial z_2}{\partial x} = 1$

以及

$\quad\dfrac{\partial z_1}{\partial y} = -\dfrac{\partial z_2}{\partial y} = k$

将上述公式替换到公式 (3) 中则有

$\quad\left.\begin{aligned}\dfrac{\partial g}{\partial z_1} + \dfrac{\partial g}{\partial z_2} &= \dfrac{\partial f}{\partial x}\\\\k\left(\dfrac{\partial g}{\partial z_1} - \dfrac{\partial g}{\partial z_2}\right) &= \dfrac{\partial f}{\partial y}\end{aligned}\ \right\} \hspace{10em}(4)$

移项之后得到

$\quad\left.\begin{aligned}\dfrac{\partial g}{\partial z_1}&= \dfrac{1}{2}\left(\dfrac{\partial f}{\partial x} + \dfrac{1}{k}\dfrac{\partial f}{\partial y}\right)\\\\\dfrac{\partial g}{\partial z_2}&= \dfrac{1}{2}\left(\dfrac{\partial f}{\partial x} - \dfrac{1}{k}\dfrac{\partial f}{\partial y}\right)\end{aligned}\ \right\} \hspace{9.3em}(5)$

上述推导中除了要求 $k$ 是一个非零复常数之外没有对它施加任何条件，因此结论是可以通用的。

现在为了证明定理一，令 $k=i$（其中 $i^2=-1$），$z_1=z$，$z_2=z^*$，那么我们可以得到以下结果：

如果 $g$ 是关于 $z$ 和 $z^*$ 的函数，并且分别对每个变量可微分，其中

$\quad z=x+iy$
$\quad z^*=x-iy$

以及

$\quad g\left(z(x, y), z^*(x, y)\right) = f(x, y)$

那么代入公式 (5) 可以发现

$\quad\left.\begin{aligned}\dfrac{\partial g}{\partial z}&= \dfrac{1}{2}\left(\dfrac{\partial f}{\partial x} - i\dfrac{\partial f}{\partial y}\right)\\\\\dfrac{\partial g}{\partial z^*}&= \dfrac{1}{2}\left(\dfrac{\partial f}{\partial x} + i\dfrac{\partial f}{\partial y}\right)\end{aligned}\ \right\} \hspace{9.7em}(6)$

从而定理一得证。

---

从定理一中我们可以直接得到一组非常重要的等式，即

$\quad\left.\begin{aligned}\dfrac{\partial z^*}{\partial z} &= \dfrac{1}{2} \left[\dfrac{\partial x}{\partial x} - i\dfrac{\partial (-iy)}{\partial y}\right] = 0\\\\\dfrac{\partial z}{\partial z^*} &= \dfrac{1}{2} \left[\dfrac{\partial x}{\partial x} + i\dfrac{\partial (iy)}{\partial y}\right] = 0\end{aligned}\ \right\}$

这意味着，在 Wirtinger derivatives 的定义下，复变量 $z$ 和 $z^*$ 可以看作两个不相关的变量，对其中一个求导时，将另一项看作常量即可。

---

假设有一个关于复变量 $z$ 的解析函数 $h$，我们可以将它写成

$\quad h(z) = g(z, z^*) = u(x, y) + iv(x, y) \hspace{5.6em}(7)$

的形式，这里 $g = h$ 没有显式地与 $z^*$ 有关，并且我们将 $f$ 分成它的实部 $u$ 和虚部 $v$，两者都是 $x$ 和 $y$ 的实值函数。

因为 $g = h$ 与 $z^*$ 无关，我们有 $\partial g / \partial z^* = 0$，而从证明中的公式 (6) 可以得到 $(\partial / \partial x + i \partial / \partial y) \cdot (u+iv)=0$ ，分别令等式左边的实部和虚部为零，得到

$\quad\left.\begin{aligned}\dfrac{\partial u}{\partial x} &= \dfrac{\partial v}{\partial y}\\\dfrac{\partial v}{\partial x} &= -\dfrac{\partial u}{\partial y}\end{aligned}\ \right\} \hspace{15em}(8)$

可以发现，定理一中其实包含了 Cauchy-Riemann 条件^[7]，即公式 (8)。

定理一很容易在一些简单的函数上进行验证。如果

$\quad\begin{aligned}g(z, z^*) &= z^2z^*\\&\textcolor{gray}{= (x+iy)^2(x-iy)=(x^3 + xy^2) + i(x^2y + y^3)}\end{aligned}$

那么有

$\quad u(x, y) = x^3 + xy^2$

$\quad v(x, y) = x^2y + y^3$

以及

$\quad\dfrac{1}{2} \left(\dfrac{\partial}{\partial x} - i\dfrac{\partial}{\partial y}\right) (u+iv) = 2(x^2 + y^2) = 2zz^* \textcolor{violet}{= \partial g / \partial z}$

$\quad\dfrac{1}{2} \left(\dfrac{\partial}{\partial x} + i\dfrac{\partial}{\partial y}\right) (u+iv) = x^2 + 2ixy + y^2 = z^2 \textcolor{violet}{= \partial g / \partial z^*}$

同理也很容易验证 $\partial z / \partial z^* = \partial z^* / \partial z = 0$ 以及 $\partial z / \partial z = \partial z^* / \partial z^* = 1$。

---

接下来，我们考虑一种常见的情况：

令 $f: \mathbb{C} \mapsto \mathbb{R}$ 是复变量 $z$（包括其共轭）的实值函数^[8]。显然，$f$ 同样等价于某个关于实变量 $x$ 和 $y$ 的实函数（其中 $z=x+iy$），但在信号处理中往往将它表示成关于 $z$ 和 $x^*$ 的实值函数会比看作 $x$ 和 $y$ 的函数更加方便。

由于 $f$（必定包含 $z^*$ 才能得到实值）看作是单个复变量 $z$ 的函数，它不是关于 $z$ 的解析函数（因为 $z \mapsto z^*$ 不是解析的），但我们假设 $f$ 满足 $g(z, z^*) = f(z)$，其中 $g$ 是两个复变量 $z$ 和 $z^*$ 的函数，并且分别是关于它们的独立的解析函数。

那么根据前面的结果，我们可以发现满足下述条件中任意一个的点都能作为 $f$ 的驻点（stationary point）：

$\quad\partial g / \partial z = 0$
$\quad\partial g / \partial z^* = 0$

也就是下一个定理。

定理二

令 $f: \mathbb{C} \mapsto \mathbb{R}$ 是复变量 $z$ 的一个实值函数。令 $f(z) = g(z, z^*)$，其中 $g: \mathbb{C} \times \mathbb{C} \mapsto \mathbb{R}$ 是关于两个复变量的函数，且满足 $g(z, a)$ 和 $g(b, z)$ 分别是 $z$ 的解析函数（$a, b \in \mathbb{C}$）。
那么 $f$ 有一个驻点的充分必要条件是 $\partial g / \partial z = 0$，其中在计算 $g$ 关于 $z$ 的偏导数时将 $z^*$ 看作常数。
类似地，也可以得到 $\partial g / \partial z^* = 0$ 也是一个充分必要条件。

〖展开以查看证明〗

令 $g\left(z(x, y), z^*(x, y)\right) = u(x, y) + iv(x, y)$，其中 $u$ 和 $v$ 都是实变函数（$\mathbb{R} \times \mathbb{R} \mapsto \mathbb{R}$）。
如果 $g$ 是实值的，那么对所有的 $x, y \in \mathbb{R}$ 都必须满足 $v(x, y) = 0$。根据公式 (6) 我们得到

$\quad\left.\begin{aligned}\dfrac{\partial g}{\partial z} &= \dfrac{1}{2} \left(\dfrac{\partial u}{\partial x} - i \dfrac{\partial u}{\partial y}\right)\\\\\dfrac{\partial g}{\partial z^*} &= \dfrac{1}{2} \left(\dfrac{\partial u}{\partial x} + i \dfrac{\partial u}{\partial y}\right)\end{aligned}\ \right\} \hspace{9.7em}(9)$

可以发现

$\quad\left.\begin{aligned}\dfrac{\partial u}{\partial x} &= \dfrac{\partial u}{\partial y} = 0 \Rightarrow \dfrac{\partial g}{\partial z} = 0\\\\\dfrac{\partial g}{\partial z} &= 0 \Rightarrow \dfrac{\partial u}{\partial x} = \dfrac{\partial u}{\partial y} = 0\end{aligned}\ \right\} \hspace{8.3em}(10)$

类似地，

$\quad\dfrac{\partial u}{\partial x} = \dfrac{\partial u}{\partial y} = 0 \Leftrightarrow \dfrac{\partial g}{\partial z^*} = 0 \hspace{9.5em}(11)$

并且 $\partial u / \partial x = \partial u / \partial y = 0$ 是 $u$（进而 $g$）有一个驻点的条件。

从公式 (10) 和 (11) 可以看出，$\partial g / \partial z = 0$ 和 $\partial g / \partial z^* = 0$ 中的任意一个条件都是 $g$ 具有一个驻点的充分必要条件，对 $f$ 也同样适用，因而定理二得证。

---

这个结果也很容易拓展到一个复向量的实值函数的情况。
我们定义 $N$ 维列向量 $\boldsymbol{z} \in \mathbb{C}^N$ 为

$\quad\boldsymbol{z} = (z_1, z_2, \cdots, z_N)^\textsf{T} \hspace{11.5em}(12)$

其中 $z_k = x_k + iy_k \ \left(x_k, y_k \in \mathbb{R}, \ k \in \{1, 2, \cdots, N\}\right)$ 以及 $\textsf{T}$ 表示矩阵转置。

我们还定义关于 $\boldsymbol{z}$ 的复梯度运算符为

$\quad\mathbf{\nabla}_{\boldsymbol{z}} = (\partial / \partial z_1, \partial / \partial z_2, \cdots, \partial / \partial z_N)^\textsf{T} \hspace{5.2em}(13)$

其中 $\partial / \partial z_k = (\partial / \partial x_k - i \partial / \partial y_k) / 2$ 与定理一证明中的公式 (6) 一致。

由此引出下一个定理。

定理三

令 $f: \mathbb{C}^N \mapsto \mathbb{R}$ 是一个关于复向量 $\boldsymbol{z}$ 的实值标量函数。令 $f(\boldsymbol{z}) = g(\boldsymbol{z}, \boldsymbol{z}^*)$，其中 $g: \mathbb{C}^N \times \mathbb{C}^N \mapsto \mathbb{R}$ 是关于两个复向量变量的实值函数，并且 $g$ 关于每个 $\boldsymbol{z}_k$ 和 $\boldsymbol{z}_k^*$ 都是解析函数。
那么 $\mathbf{\nabla}_{\boldsymbol{z}} g = \mathbf{0}$ 和 $\mathbf{\nabla}_{\boldsymbol{z}^*} g = \mathbf{0}$ 两者中的任意一个都是使得 $f$ 有一个驻点的充分必要条件。

〖展开以查看证明〗

我们可以将 $f$ 表示成关于 $2N$ 个变量 $x_k, y_k$ 的一个实变函数 $u$，并且当且仅当 $\partial u / \partial x_k = \partial u / \partial y_k = 0$ 对所有 $k$ 都成立时， $u$（进而 $f$）有一个驻点。

根据公式 (9) 和紧随其后的定理二的证明，上面的条件等价于：当且仅当 $\partial g / \partial z_k = 0$ 对所有 $k$ 都成立，也就是当且仅当 $\mathbf{\nabla}_{\boldsymbol{z}} g = \mathbf{0}$。

类似地，$\mathbf{\nabla}_{\boldsymbol{z}^*} g = \mathbf{0}$（即 $\partial g / \partial z_k^* = 0$ 对所有 $k$ 都成立）也是一个充分必要条件。因此定理三得证。

---

最后我们再考虑复梯度的理解或者含义问题。如果按照定理二对 $g$ 进行定义，由 $g$ 的一阶 Taylor 展开可以得到：

$\quad\begin{aligned}\delta g &= \dfrac{\partial g}{\partial z} \delta z + \dfrac{\partial g}{\partial z^*} \delta z^* \\&\textcolor{gray}{= \dfrac{1}{2} \left(\dfrac{\partial u}{\partial x} - i \dfrac{\partial u}{\partial y}\right) (\delta x + i\delta y) +}\\&\hspace{1.4em} \textcolor{gray}{\dfrac{1}{2} \left(\dfrac{\partial u}{\partial x} + i \dfrac{\partial u}{\partial y}\right) (\delta x - i\delta y)} \\&\textcolor{gray}{= \dfrac{\partial u}{\partial x} \delta x + \dfrac{\partial u}{\partial y} \delta y}\\&= 2 \operatorname{Re}\left(\dfrac{\partial g}{\partial z} \delta z\right)\hspace{12.35em}(14)\end{aligned}$

如果 $g$ 是如定理三中定义的关于复向量的一个实值标量函数，那么

$\quad\begin{aligned}\delta g &= \sum_k \left(\dfrac{\partial g}{\partial z_k} \delta z_k + \dfrac{\partial g}{\partial z_k^*} \delta z_k^*\right)\\&=(\mathbf{\nabla}_{\boldsymbol{z}} g)^\textsf{T} \delta \boldsymbol{z} + (\mathbf{\nabla}_{\boldsymbol{z}^*} g)^\textsf{T} \delta \boldsymbol{z}^*\\&= 2\operatorname{Re}\left[(\mathbf{\nabla}_{\boldsymbol{z}} g)^\textsf{T} \delta \boldsymbol{z}\right]\\&= 2\operatorname{Re}\left[(\mathbf{\nabla}_{\boldsymbol{z}^*} g)^\textsf{H} \delta \boldsymbol{z}\right] \hspace{10.4em}(15)\end{aligned}$

上述推导中我们利用了 $\textcolor{maroon}{\mathbf{\nabla}_{\boldsymbol{z}^*} g = (\mathbf{\nabla}_{\boldsymbol{z}} g)^*}$（因为这些运算符在 $g$ 是实值时互为复共轭），$\textsf{T}$ 和 $\textsf{H}$ 分别表示矩阵转置和复共轭转置。

由于两个 $N$ 维向量 $\boldsymbol{a}$ 和 $\boldsymbol{b}$ 的积 $\boldsymbol{a}^\textsf{H} \boldsymbol{b}$ 满足内积 $(\boldsymbol{a}, \boldsymbol{b})$ 的公理（axioms）^[9]，我们可以应用 Schwarz 不等式：

$\quad |(\boldsymbol{a}, \boldsymbol{b})| \le \|\boldsymbol{a}\| \, \|\boldsymbol{b}\|$

其中 $\|\boldsymbol{a}\|$ 是 $\boldsymbol{a}$ 的范数或者幅度，在这里有 $\|\boldsymbol{a}\|^2 = \sum_k |a_k|^2$

等号仅当 $\boldsymbol{b} = \ell \boldsymbol{a}$ 时成立，其中 $\ell$ 是一个标量，并且可能是复数（此时有 $(\boldsymbol{a}, \boldsymbol{b}) = \ell \|\boldsymbol{a}\|^2$）。

因此对于给定 $\|\boldsymbol{a}\|$ 和 $\|\boldsymbol{b}\|$ 取值的情况，我们可以推出 $\operatorname{Re}[(\boldsymbol{a}, \boldsymbol{b})]$ 的最大值出现在 $k$ 是正实数时，即当 $\boldsymbol{a}$ 和 $\boldsymbol{b}$（在向量空间 $\mathbb{C}^N$ 中）同方向时。

如果分别用 $\mathbf{\nabla}_{\boldsymbol{z}^*} g$ 替换 $\boldsymbol{a}$ 和用 $\delta \boldsymbol{z}$ 替换 $\boldsymbol{b}$，我们可以看到对于一个给定幅度的 $\delta \boldsymbol{z}$，$g$（进而 $f$，其中 $f(\bold{z}) = g(\boldsymbol{z}, \boldsymbol{z}^*)$）取值的最大变化出现在 $\delta \boldsymbol{z}$ 与 $\mathbf{\nabla}_{\boldsymbol{z}^*} g$ 同方向时。由此引出下一个定理。

---

定理四

给定定理三中定义的 $f$ 和 $g$，梯度 $\mathbf{\nabla}_{\boldsymbol{z}^*} g$ 定义了 $f$ 随着 $\boldsymbol{z}$ 变化的最大速率的方向。对于一个变化的极小量 $\delta \boldsymbol{z}$，$f$ 值的变化是：

$\quad\delta f = 2 \operatorname{Re}\left[(\mathbf{\nabla}_{\boldsymbol{z}^*} g)^\textsf{H} \delta \boldsymbol{z}\right] \hspace{10.32em}(16)$

---

常见实值标量函数的复梯度结果

公式 (13) 中定义的关于一个 $N$ 维复向量 $\boldsymbol{z}$ 的复梯度运算符 $\mathbf{\nabla}_\boldsymbol{z}$ 会从关于 $\boldsymbol{z}$ 的标量函数 $f$ 中生成另一个 $N$ 维复向量。通常来说，这个标量函数是复函数，当然在信号处理的实际应用中它经常是实函数，如表示成 $\boldsymbol{a}^\textsf{H} \boldsymbol{z}$ 或者 $\boldsymbol{z}^\textsf{H} \mathbf{R} \boldsymbol{z}$ 等类似功率的物理量形式，其中 $\mathbf{R}$ 通常是 Hermitian 矩阵（即 $\mathbf{R} = \mathbf{R}^\textsf{H}$），并且 $\boldsymbol{a}$ 和 $\mathbf{R}$ 是与 $\boldsymbol{z}$ 无关的常量。

因此，大部分情况下我们只需要处理 $\boldsymbol{a}^\textsf{H}\boldsymbol{z}$, $\boldsymbol{z}^\textsf{H}\boldsymbol{a}$ 和 $\boldsymbol{z}^\textsf{H}\mathbf{R}\boldsymbol{z}$ 这三种标量函数。

对它们取 $\mathbf{\nabla}_{\boldsymbol{z}}$ 或者 $\mathbf{\nabla}_{\boldsymbol{z}^*}$（分别对应 $\partial / \partial z_k$ 和 $\partial / \partial z_k^*$）， 利用以下关系：

• $\partial z_k / \partial z_k = 1$ 和它的共轭版本
• $\partial z_k / \partial z_k^* = 0$ 和它的共轭版本
• $\partial u_j / \partial v_k = 0\ (j \neq k)$，其中 $u$ 和 $v$ 可能是 $\boldsymbol{z}$ 和 $\boldsymbol{z}^*$ 中的任意一个

我们可以得到

$\textcolor{maroon}{\mathbf{\nabla}=\mathbf{\nabla}_{\mathbf{z}^*}}$	$\textcolor{maroon}{\mathbf{\nabla}=\mathbf{\nabla}_{\mathbf{z}}}$
$\mathbf{\nabla} (\boldsymbol{a}^\textsf{H} \boldsymbol{z}) = \mathbf{0}$	$\mathbf{\nabla} (\boldsymbol{a}^\textsf{H} \boldsymbol{z}) = \boldsymbol{a}^* \hspace{12em}(17a)$
$\mathbf{\nabla} (\boldsymbol{z}^\textsf{H} \boldsymbol{a}) = \boldsymbol{a}$	$\mathbf{\nabla} (\boldsymbol{z}^\textsf{H} \boldsymbol{a}) = \mathbf{0} \hspace{12.6em}(17b)$
$\mathbf{\nabla} (\boldsymbol{z}^\textsf{H} \mathbf{R} \boldsymbol{z}) = \mathbf{R}\boldsymbol{z}$	$\mathbf{\nabla} (\boldsymbol{z}^\textsf{H} \mathbf{R} \boldsymbol{z}) = \mathbf{R}^\textsf{T}\boldsymbol{z}^* = \left(\mathbf{R}^\textsf{H} \boldsymbol{z}\right)^* \hspace{5em}(17c)$

〖展开以查看证明〗

【公式 (17a) 证明】
令 $f(\boldsymbol{z}) = g(\boldsymbol{z}, \boldsymbol{z}^*) = \boldsymbol{a}^\textsf{H} \boldsymbol{z}$ 是关于 $\boldsymbol{z}$ 的实值函数，$\boldsymbol{a}$ 是与 $\boldsymbol{z}$ 无关的 $N$ 维复向量。

我们进一步将 $f$ 写成关于 $2N$ 个复变量的实值函数 $u(z_1, z_1^*, z_2, z_2^*, \cdots, z_N, z_N^*)$（$k \in \{1, 2, \cdots, N\}$）。

那么可以得到

$\quad u(z_1, z_1^*, z_2, z_2^*, \cdots, z_N, z_N^*) = \sum_k a_k^* z_k$

$\quad\left.\begin{aligned}\dfrac{\partial u}{\partial z_k^*} &= \dfrac{\partial (a_k^* z_k)}{\partial z_k^*} = 0\\\\\dfrac{\partial u}{\partial z_k} &= \dfrac{\partial (a_k^* z_k)}{\partial z_k} = a^*_k\end{aligned}\ \right\}\ \Rightarrow\ \left.\begin{aligned}\mathbf{\nabla}_{\boldsymbol{z}^*} (\boldsymbol{a}^\textsf{H} \boldsymbol{z}) &= \mathbf{0}\\\\\mathbf{\nabla}_{\boldsymbol{z}} (\boldsymbol{a}^\textsf{H} \boldsymbol{z}) &= \boldsymbol{a}^*\end{aligned}\ \right\}$

---

【公式 (17b) 证明】

类似地，可以得到

$\quad u(z_1, z_1^*, z_2, z_2^*, \cdots, z_N, z_N^*) = \sum_k a_k z_k^*$

$\quad\left.\begin{aligned}\dfrac{\partial u}{\partial z_k^*} &= \dfrac{\partial (a_k z_k^*)}{\partial z_k^*} = a_k\\\\\dfrac{\partial u}{\partial z_k} &= \dfrac{\partial (a_k z_k^*)}{\partial z_k} = 0\end{aligned}\ \right\}\ \Rightarrow\ \left.\begin{aligned}\mathbf{\nabla}_{\boldsymbol{z}^*} (\boldsymbol{a}^\textsf{H} \boldsymbol{z}) &= \boldsymbol{a}\\\\\mathbf{\nabla}_{\boldsymbol{z}} (\boldsymbol{a}^\textsf{H} \boldsymbol{z}) &= \mathbf{0}\end{aligned}\ \right\}$

---

【公式 (17c) 证明】

类似地，可以得到

$\quad \mathbf{R} \boldsymbol{z} = \left(\sum_l R_{1l}z_l, \sum_l R_{2l}z_l, \cdots, \sum_l R_{Nl}z_l\right)^\textsf{T}$

$\quad \mathbf{R}^\textsf{H} \boldsymbol{z} = \left(\sum_k R^*_{k1}z_k, \sum_k R^*_{k2}z_k, \cdots, \sum_k R^*_{kN}z_k\right)^\textsf{T}$

$\quad u(z_1, z_1^*, z_2, z_2^*, \cdots, z_N, z_N^*) = \sum_l \sum_k z^*_k R_{kl} z_l$

$\quad\left.\begin{aligned}\dfrac{\partial u}{\partial z_k^*} &= \dfrac{\partial (\sum_l \sum_k z^*_k R_{kl} z_l)}{\partial z_k^*} = \sum_l R_{kl} z_l\\\\\dfrac{\partial u}{\partial z_l} &= \dfrac{\partial (\sum_l \sum_k z^*_k R_{kl} z_l)}{\partial z_l} = \sum_k z^*_k R_{kl}\end{aligned}\ \right\}\ \Rightarrow\ \left.\begin{aligned}\mathbf{\nabla}_{\boldsymbol{z}^*} (\boldsymbol{z}^\textsf{H} \mathbf{R} \boldsymbol{z}) &= \mathbf{R}\boldsymbol{z}\\\\\mathbf{\nabla}_{\boldsymbol{z}} (\boldsymbol{z}^\textsf{H} \mathbf{R} \boldsymbol{z}) &= \left(\mathbf{R}^\textsf{H} \boldsymbol{z}\right)^*\end{aligned}\ \right\}$

---

有了上述结果，任意一个相似的标量函数都可以整理成合适的形式，从而能够直接应用上述结论。比如

• 将公式 (17a) 中的 $\boldsymbol{a}$ 替换为 $\boldsymbol{a}^*$
• 将公式 (17b) 中的 $\boldsymbol{z}$ 与 $\boldsymbol{z}^*$ 互换

即可得到

$\textcolor{maroon}{\mathbf{\nabla}=\mathbf{\nabla}_{\mathbf{z}^*}}$	$\textcolor{maroon}{\mathbf{\nabla}=\mathbf{\nabla}_{\mathbf{z}}}$
$\mathbf{\nabla} (\boldsymbol{a}^\textsf{T} \boldsymbol{z}) = \mathbf{0}$	$\mathbf{\nabla} (\boldsymbol{a}^\textsf{T} \boldsymbol{z}) = \boldsymbol{a}$
$\mathbf{\nabla} (\boldsymbol{z}^\textsf{T} \boldsymbol{a}) = \mathbf{0}$	$\mathbf{\nabla} (\boldsymbol{z}^\textsf{T} \boldsymbol{a}) = \boldsymbol{a}$

观察公式 (17a)–(17c)，我们能够发现 $\mathbf{\nabla}_{\boldsymbol{z}^*}$ 的结果看起来要比 $\mathbf{\nabla}_{\boldsymbol{z}}$ 稍微齐整一些。而根据定理三，这两者任意一个都能决定驻点的条件，因此通常采用 $\mathbf{\nabla}_{\boldsymbol{z}^*}$ 就足够了。
在后面的讨论中，除非明确标注了 $\mathbf{\nabla}_{\boldsymbol{z}}$，我们也默认采用 $\mathbf{\nabla} = \mathbf{\nabla}_{\boldsymbol{z}^*}$ 并省略掉下标 $\boldsymbol{z}^*$。

其实从定理四中我们也能看到，对应 $f$ 最大变化速率的方向的是关于 $\boldsymbol{z}^*$ 的梯度，而不是关于 $\boldsymbol{z}$ 的梯度。

---

*与实梯度运算符的关系

有了上面定义的复梯度运算符，我们就可以将它与以前常用的实数域的梯度运算符进行比较，从而明确两者间的不同。

关于实梯度运算符的计算方式，可以参考文献 [R6] 和 [R7]。

值得注意的是，如果我们简单地将实梯度运算符的结果中的实变量替换成复变量，它未必会等于复梯度运算符的结果。比如

复梯度运算符	实梯度运算符
$\mathbf{\nabla}_{\boldsymbol{z}} (\boldsymbol{z}^\textsf{H} \boldsymbol{z}) = \boldsymbol{z}^* \hspace{7em}(18)$	$\mathbf{\nabla}_{\boldsymbol{x}} (\boldsymbol{x}^\textsf{T} \boldsymbol{x}) = 2\boldsymbol{x} \hspace{7em}(19)$
$\mathbf{\nabla}_{\boldsymbol{z}} (\boldsymbol{z}^\textsf{T} \boldsymbol{z}) = 2\boldsymbol{z}$	-
$\mathbf{\nabla}_{\boldsymbol{z}} (\boldsymbol{z}^\textsf{H} \boldsymbol{z}^*) = \mathbf{0}$	-

复梯度运算符	实梯度运算符
情形 (1): 关于 $\boldsymbol{z}$ 的复函数: $\mathbf{\nabla}_{\boldsymbol{z}}(\boldsymbol{a}^\textsf{T} \boldsymbol{z} + \boldsymbol{z}^\textsf{T} \boldsymbol{a}) = \mathbf{\nabla}_{\boldsymbol{z}}(2\boldsymbol{a}^\textsf{T} \boldsymbol{z}) = 2\boldsymbol{a}$	$\mathbf{\nabla}_{\boldsymbol{x}}(\boldsymbol{a}^\textsf{T} \boldsymbol{x} + \boldsymbol{x}^\textsf{T} \boldsymbol{a}) = \mathbf{\nabla}_{\boldsymbol{x}}(2\boldsymbol{a}^\textsf{T} \boldsymbol{x}) = 2\boldsymbol{a}$
情形 (2): 关于 $\boldsymbol{z}$ 和 $\boldsymbol{z}^*$ 的实函数: $\mathbf{\nabla}_{\boldsymbol{z}}(\boldsymbol{a}^\textsf{T} \boldsymbol{z} + \boldsymbol{z}^\textsf{H} \boldsymbol{a}) = \boldsymbol{a}$	-
情形 (3): 关于 $\boldsymbol{z}^*$ 的复函数: $\mathbf{\nabla}_{\boldsymbol{z}}(\boldsymbol{a}^\textsf{T} \boldsymbol{z}^* + \boldsymbol{z}^\textsf{H} \boldsymbol{a}) = \mathbf{\nabla}_{\boldsymbol{z}}(2\boldsymbol{a}^\textsf{T} \boldsymbol{z}^*) = \mathbf{0}$	-

复梯度运算符	实梯度运算符
情形 (1): 关于 $\boldsymbol{z}$ 的复函数: $\begin{aligned}\mathbf{\nabla}_{\boldsymbol{z}}(\boldsymbol{z}^\textsf{T} \mathbf{R} \boldsymbol{z}) &= (\boldsymbol{z}^\textsf{T} \mathbf{R})^\textsf{T} + \mathbf{R}\boldsymbol{z}\\&=(\mathbf{R}^\textsf{T} + \mathbf{R})\boldsymbol{z}\\&= 2\operatorname{Re}(\mathbf{R})\boldsymbol{z}\ \textcolor{tan}{(\text{if} \ \mathbf{R} \ \text{is Hermitian})}\end{aligned}$	$\begin{aligned}\mathbf{\nabla}_{\boldsymbol{x}}(\boldsymbol{x}^\textsf{T} \mathbf{A} \boldsymbol{x}) &= (\boldsymbol{x}^\textsf{T} \mathbf{A})^\textsf{T} + \mathbf{A}\boldsymbol{x} = (\mathbf{A}^{\textsf{T}} + \mathbf{A}) \boldsymbol{x}\\&= 2\mathbf{A}\boldsymbol{x} \ \textcolor{tan}{(\text{if } \mathbf{A} \ \text{is symmetric})}\end{aligned}$
情形 (2): 关于 $\boldsymbol{z}$ 和 $\boldsymbol{z}^*$ 的实函数: $\begin{aligned}\mathbf{\nabla}_{\boldsymbol{z}}(\boldsymbol{z}^\textsf{H} \mathbf{R} \boldsymbol{z}) &= (\boldsymbol{z}^\textsf{H} \mathbf{R})^\textsf{T}\\&=\mathbf{R}^\textsf{T}\boldsymbol{z}^*\\&= \mathbf{R}^*\boldsymbol{z}^*\ \textcolor{tan}{(\text{if} \ \mathbf{R} \ \text{is Hermitian})}\end{aligned}$	-

其中 $\boldsymbol{x} \in \mathbb{R}^N$，$\mathbf{\nabla}_{\boldsymbol{x}} = \left(\partial / \partial x_1, \partial / \partial x_2, \cdots, \partial / \partial x_N\right)^\textsf{T}$，$\boldsymbol{a} \in \mathbb{R}^N$，$\mathbf{A} \in \mathbb{R}^{N \times N}$，以及 $\mathbf{R} \in \mathbb{C}^{N \times N}$。

从上述结果以及公式 (17c) 可以发现，信号处理文献中常常误认为的

• 与 $\mathbf{\nabla} (\boldsymbol{x}^\textsf{T} \mathbf{A} \boldsymbol{x}) = 2\mathbf{A}\boldsymbol{x}$ 相对应的复梯度结果是 $\mathbf{\nabla}(\boldsymbol{z}^\textsf{H} \mathbf{R} \boldsymbol{z}) = 2\mathbf{R}\boldsymbol{z}$

实际上等价于这里定义的 $2 \mathbf{\nabla}_{\boldsymbol{z}^*}$。

当然，这里引入的系数 2 并不会导致错误的结果，因为所有的梯度都按照这个系数被放大。

---

复梯度运算符的基本性质

线性

如果 $f$ 和 $h$ 都是关于 $N$ 维复向量 $\boldsymbol{z}$ 的实值函数，$\alpha$ 和 $\beta$ 是复数常量，则对于所有 $k\in\{1, 2, \cdots, N\}$ 下式都成立：

$\quad\dfrac{\partial}{\partial z_k}(\alpha f + \beta h) = \alpha \dfrac{\partial f}{\partial z_k} + \beta \dfrac{\partial h}{\partial z_k}$

如果 $f$ 和 $h$ 都是关于 $N$ 维复向量 $\boldsymbol{z}^*$ 的实值函数，$\alpha$ 和 $\beta$ 是复数常量，则对于所有 $k\in\{1, 2, \cdots, N\}$ 下式都成立：

$\quad\dfrac{\partial}{\partial z_k^*}(\alpha f + \beta h) = \alpha \dfrac{\partial f}{\partial z_k^*} + \beta \dfrac{\partial h}{\partial z_k^*}$

乘法法则

如果 $f$ 和 $h$ 都是关于 $N$ 维复向量 $\boldsymbol{z}$ 的实值函数，则对于所有 $k\in\{1, 2, \cdots, N\}$ 下式都成立：

$\quad\dfrac{\partial}{\partial z_k}(f \cdot h) = \dfrac{\partial f}{\partial z_k} \cdot g + f \cdot \dfrac{\partial h}{\partial z_k}$

如果 $f$ 和 $h$ 都是关于 $N$ 维复向量 $\boldsymbol{z}^*$ 的实值函数，则对于所有 $k\in\{1, 2, \cdots, N\}$ 下式都成立：

$\quad\dfrac{\partial}{\partial z_k^*}(f \cdot h) = \dfrac{\partial f}{\partial z_k^*} \cdot g + f \cdot \dfrac{\partial h}{\partial z_k^*}$

链式法则

如果 $f$ 和 $h$ 都是关于 $N$ 维复向量 $\boldsymbol{z}$ 的实值函数，则对于所有 $k\in\{1, 2, \cdots, N\}$ 下式都成立：

$\quad\dfrac{\partial}{\partial z_k}(f \circ h) = \sum\limits_{i=1}^N \left(\dfrac{\partial f}{\partial z_i} \circ h\right) \dfrac{\partial h_i}{\partial z_k} + \sum\limits_{i=1}^N \left(\dfrac{\partial f}{\partial z_i^*} \circ h\right) \dfrac{\partial h_i^*}{\partial z_k}$

如果 $h$ 是关于 $\boldsymbol{z}$ 的解析函数，那么上式中的第二项变成 $\mathbf{0}$，上述链式法则也退化成我们所熟知的普通链式法则。

如果 $f$ 和 $h$ 都是关于 $N$ 维复向量 $\boldsymbol{z}^*$ 的实值函数，则对于所有 $k\in\{1, 2, \cdots, N\}$ 下式都成立：

$\quad\dfrac{\partial}{\partial z_k^*}(f \circ h) = \sum\limits_{i=1}^N \left(\dfrac{\partial f}{\partial z_i} \circ h\right) \dfrac{\partial h_i}{\partial z_k^*} + \sum\limits_{i=1}^N \left(\dfrac{\partial f}{\partial z_i^*} \circ h\right) \dfrac{\partial h_i^*}{\partial z_k^*}$

如果 $h$ 是关于 $\boldsymbol{z}^*$ 的解析函数，那么上式中的第二项变成 $\mathbf{0}$，上述链式法则也退化成我们所熟知的普通链式法则。

其中 $f \circ h$ 表示复合函数，即 $(f \circ h)(\boldsymbol{z}) = f(h(\boldsymbol{z}))$^[10]。

共轭

如果 $f$ 是关于 $N$ 维复向量 $\boldsymbol{z}$ 的实值函数，则对于所有 $k\in\{1, 2, \cdots, N\}$ 下式都成立：

$\quad\left(\dfrac{\partial f}{\partial z_k}\right)^* = \dfrac{\partial f^*}{\partial z_k^*}$

如果 $f$ 是关于 $N$ 维复向量 $\boldsymbol{z}^*$ 的实值函数，则对于所有 $k\in\{1, 2, \cdots, N\}$ 下式都成立：

$\quad\left(\dfrac{\partial f}{\partial z_k^*}\right)^* = \dfrac{\partial f^*}{\partial z_k}$

---

复梯度运算符的应用实例

应用一

自适应阵列理论中常常遇到的一个典型问题类型是

• 在满足以下条件的情况下使得正实数量 $\boldsymbol{w}^\textsf{H} \mathbf{R} \boldsymbol{w}$ 最小：

$\qquad\boldsymbol{w}^\textsf{H} \boldsymbol{c} = a \hspace{16.2em}(20)$

这里 $\boldsymbol{w}^\textsf{H} \mathbf{R} \boldsymbol{w}$ 是阵列输出功率的表达形式，$N$ 维复向量 $\boldsymbol{w}$ 是对应 $N$ 元阵列的滤波器，$N \times N$ 维的 Hermitian 矩阵 $\mathbf{R}$ 是阵列信号的协方差矩阵。

公式 (20) 的条件防止了求解过程中找到平凡解 $\boldsymbol{w}=\mathbf{0}$，并且它的含义是为滤波器等于 $\boldsymbol{w}=\boldsymbol{c}$ 时的阵列设置一个固定的幅度增益 $a$。（通常 $\boldsymbol{c}$ 对应于决定阵列指向的导向向量 (steering vector)）
通常 $a$ 取一个实数常量（如 1 或者 $N$），但是理论上也可以是复数，这里我们考虑这种一般的情况。

求解这个问题的典型方法就是采用 Lagrange 乘子法和一个合适的损失函数。因为这里我们想要利用前面的定理三，我们需要定义一个实值损失函数，即

$\quad\begin{aligned}H(\boldsymbol{w}, \boldsymbol{w}^*) &= \boldsymbol{w}^\textsf{H} \mathbf{R} \boldsymbol{w} + 2\operatorname{Re}\left[\lambda (\boldsymbol{w}^\textsf{H} \boldsymbol{c} - a)\right] \hspace{2.05em}(21)\\&= \boldsymbol{w}^\textsf{H} \mathbf{R} \boldsymbol{w} + \lambda (\boldsymbol{w}^\textsf{H}\boldsymbol{c} - a) + \lambda^* (\boldsymbol{c}^\textsf{H}\boldsymbol{w} - a^*)\end{aligned}$

上面公式中的系数 2 并不是必要的（只是对 $\lambda$ 的缩放），这里加上它可以和后续化简时出现的 1/2 抵消掉。

根据定理三，$\mathbf{\nabla} H = \mathbf{0}$ 对应 $H$ 的驻点（这一节中默认 $\mathbf{\nabla} = \mathbf{\nabla}_{\boldsymbol{z}^*}$）。对照公式 (17) 中的规则对公式 (21) 求导，可以得到

$\quad\mathbf{\nabla} H = \mathbf{R}\boldsymbol{w} + \lambda \boldsymbol{c}$

假设当 $\mathbf{\nabla} H = \mathbf{0}$ 时 $\boldsymbol{w} = \boldsymbol{w}_0$，则有

$\quad\mathbf{R}\boldsymbol{w}_0 = -\lambda \boldsymbol{c} \hspace{15.55em}(22)$

或者（如果 $\mathbf{R}$ 可逆）

$\quad\boldsymbol{w}_0 = -\lambda \mathbf{R}^{-1} \boldsymbol{c} \hspace{14.5em}(23)$

又因为 $\boldsymbol{w}_0$ 满足公式 (20) 给出的条件，我们有

$\quad\boldsymbol{c}^\textsf{H}\boldsymbol{w}_0 = a^* = -\lambda \boldsymbol{c}^\textsf{H} \mathbf{R}^{-1} \boldsymbol{c}$

或者（因为 $\boldsymbol{c}^\textsf{H} \mathbf{R}^{-1} \boldsymbol{c}$ 是标量）

$\quad\lambda = -a^* / (\boldsymbol{c}^\textsf{H} \mathbf{R}^{-1} \boldsymbol{c}) \hspace{12.25em}(24)$

从公式 (23) 和 (24) 中我们可以发现，上述优化问题的解是

$\quad\boxed{\boldsymbol{w}_0 = \dfrac{a^* \mathbf{R}^{-1} \boldsymbol{c}}{\boldsymbol{c}^\textsf{H} \mathbf{R}^{-1} \boldsymbol{c}}} \hspace{13.9em}(25)$

并且 $f(\boldsymbol{w}) = \boldsymbol{w}^\textsf{H} \mathbf{R} \boldsymbol{w}$ 的最小值是

$\quad\begin{aligned}f(\boldsymbol{w}_0) &= \boldsymbol{w}_0^\textsf{H} \mathbf{R} \boldsymbol{w}_0 = -\lambda \boldsymbol{w}_0^\textsf{H} \boldsymbol{c} = -\lambda a\\&= |a|^2 / (\boldsymbol{c}^\textsf{H} \mathbf{R}^{-1} \boldsymbol{c})\end{aligned} \hspace{4.8em}(26)$

注意到 $\boldsymbol{c}^\textsf{H} \mathbf{R}^{-1} \boldsymbol{c}$ 其实是实数，因为 Hermitian 矩阵的逆 $\mathbf{R}^{-1}$ 也是 Hermitian 矩阵。$f(\boldsymbol{w}_0)$ 的取值也因为一定是实数。

应用二

第二个例子同样是最小化阵列输出功率 $\boldsymbol{w}^\textsf{H} \mathbf{R} \boldsymbol{w}$，但约束条件改为

$\quad \boldsymbol{w}^\textsf{H} \boldsymbol{w} = a \hspace{16.85em}(27)$

其中 $a$ 是一个正实数，它通过约束滤波器的范数来确保不会出现平凡解 $\boldsymbol{w} = \mathbf{0}$。

这种情况下，Lagrange 乘子法的损失函数为

$\quad H(\boldsymbol{w}, \boldsymbol{w}^*) = \boldsymbol{w}^\textsf{H} \mathbf{R} \boldsymbol{w} + \lambda(\boldsymbol{w}^\textsf{H} \boldsymbol{w} - a) \hspace{4.95em}(28)$

因为约束条件是实数以及 $H$ 是实值函数，那么一定有 $\lambda$ 也是实数。

对公式 (28) 求导，得到

$\quad \mathbf{\nabla} H = \mathbf{R} \boldsymbol{w} + \lambda \boldsymbol{w} \hspace{13.3em}(29)$

如果 $\boldsymbol{w} = \boldsymbol{w}_0$ 是驻点（$\mathbf{\nabla}H = \mathbf{0}$），那么

$\quad\boxed{\mathbf{R} \boldsymbol{w}_0 = -\lambda \boldsymbol{w}_0} \hspace{14.05em}(30)$

这表明此问题的最优滤波器 $\boldsymbol{w}_0$ 是协方差矩阵 $\mathbf{R}$ 的一个特征向量。

应用三

最小均方（LMS）滤波器的目标是最小化阵列输出和目标信号（参考信号）之间的均方误差（或者误差信号的功率）。文献 [R8] 将原始的 Widrow-Hoff LMS 算法拓展到复信号时，采用的是分别对实部和虚部计算梯度的方式。这里我们可以用类似前面的方法来更简洁地表示复数梯度。

令第 $j$ 个样本点时刻的滤波器为 $\boldsymbol{w}_j$，$N$ 元阵列信号在时刻 $j$ 为 $\boldsymbol{x}_j$，那么时刻 $j$ 的阵列输出可表示为

$\quad y_j = \boldsymbol{x}_j^\textsf{T} \boldsymbol{w}_j = \boldsymbol{w}_j^\textsf{T} \boldsymbol{x}_j \hspace{12.2em}(31)$

令目标信号为 $d_j$，那么误差信号可以表示为

$\quad e_j = d_j - y_j = d_j - \boldsymbol{x}_j^\textsf{T} \boldsymbol{w}_j \hspace{9.4em}(32)$

文献 [R8] 中称滤波器向量应该优化的方向是与误差功率 $e_j e_j^*$ 最大瞬时增长速率相反的方向（这就是最速下降法）。因此下一时刻的滤波器向量 $\boldsymbol{w}_{j+1}$ 应计算如下：

$\quad\boldsymbol{w}_{j+1} = \boldsymbol{w}_{j} -\mu \mathbf{\nabla}(e_j e_j^*) \hspace{10.45em}(33)$

其中 $\mu$ 是一个正实数。

根据链式法则，我们有

$\quad\mathbf{\nabla} (e_j e_j^*) = e_j \mathbf{\nabla} e_j^* + (\mathbf{\nabla} e_j) e_j^* \hspace{8em}(34)$

结合公式 (32) 和 公式 (17)，我们可以得到

$\quad\mathbf{\nabla} e_j^* = \mathbf{\nabla} \left(d_j^* - \boldsymbol{w}_j^\textsf{H} \boldsymbol{x}_j^*\right) = -\boldsymbol{x}_j^*$

以及

$\quad\mathbf{\nabla} e_j = \mathbf{0}$

再结合公式 (33) 和 (34)，我们得到如下关系

$\quad\boxed{\boldsymbol{w}_{j+1} = \boldsymbol{w}_j + \mu e_j \boldsymbol{x}_j^*} \hspace{11.45em}(35)$

这一结果与文献 [R8] 中的公式 (16) 一致（除了少了一个对 $\mu$ 产生缩放的系数 2）。

复标量函数关于复矩阵的偏导数

基本定义

进一步地，我们将上述定义拓展到关于复矩阵的标量函数。

我们定义 $N \times Q$ 维矩阵变量 $\mathbf{Z} \in \mathbb{C}^{N \times Q}$ 为

$\quad\mathbf{Z} = \begin{bmatrix}z_{1,1} & z_{1,2} & \cdots & z_{1,Q}\\z_{2,1} & z_{2,2} & \cdots & z_{2,Q}\\\vdots & \vdots & \ddots & \vdots\\z_{N,1} & z_{N,2} & \cdots & z_{N,Q}\end{bmatrix} \hspace{7.25em}(36)$

其中 $z_{k,l} = x_{k,l} + iy_{k,l} \ \left(x_{k,l}, y_{k,l} \in \mathbb{R}, \ k \in \{1, 2, \cdots, N\}, \ l \in \{1, 2, \cdots, Q\}\right)$。$\mathbf{Z} = \mathbf{X} + i \mathbf{Y}$，$\mathbf{X}, \mathbf{Y} \in \mathbb{R}^{N \times Q}$。

我们还定义关于矩阵 $\mathbf{Z}$ 的复梯度运算符为

$\quad\mathbf{\nabla}_{\mathbf{Z}} = \begin{bmatrix}\frac{\partial}{\partial z_{1,1}} & \frac{\partial}{\partial z_{1,2}} & \cdots & \frac{\partial}{\partial z_{1,Q}}\\[5pt]\frac{\partial}{\partial z_{2,1}} & \frac{\partial}{\partial z_{2,2}} & \cdots & \frac{\partial}{\partial z_{2,Q}}\\[5pt]\vdots & \vdots & \ddots & \vdots\\[5pt]\frac{\partial}{\partial z_{N,1}} & \frac{\partial}{\partial z_{N,2}} & \cdots & \frac{\partial}{\partial z_{N,Q}}\end{bmatrix} \hspace{5.63em}(37)$

其中 $\partial / \partial z_{k,l} = (\partial / \partial x_{k,l} - i \partial / \partial y_{k,l}) / 2$ 与定理一证明中的公式 (6) 一致。

此外，我们也可以按照复微分的定义写出相应的复微分关系式：

$\quad \operatorname{d}\!z_{k,l} = \operatorname{d}\!x_{k,l} + i\operatorname{d}\!y_{k,l}$
$\quad \operatorname{d}\!z^*_{k,l} = \operatorname{d}\!x_{k,l} - i\operatorname{d}\!y_{k,l}$
$\quad \operatorname{d}\!z^*_{k,l} = (\operatorname{d}\!z_{k,l})^*$

$\quad\begin{aligned}\operatorname{d}\!f &= \sum_{k=1}^N\sum_{l=1}^Q\dfrac{\partial f}{\partial x_{k,l}} \operatorname{d}\!x_{k,l} + \sum_{k=1}^N\sum_{l=1}^Q\dfrac{\partial f}{\partial y_{k,l}} \operatorname{d}\!y_{k,l} \\[15pt]&= \sum_{k=1}^N\sum_{l=1}^Q\dfrac{\partial f}{\partial x_{k,l}} \dfrac{\operatorname{d}\!z_{k,l} + \operatorname{d}\!z^*_{k,l}}{2} + \sum_{k=1}^N\sum_{l=1}^Q\dfrac{\partial f}{\partial y_{k,l}} \dfrac{\operatorname{d}\!z_{k,l} - \operatorname{d}\!z^*_{k,l}}{2i} \\[15pt]&= \sum_{k=1}^N\sum_{l=1}^Q\dfrac{1}{2}\left(\dfrac{\partial f}{\partial x_{k,l}} - i \dfrac{\partial f}{\partial y_{k,l}}\right)\operatorname{d}\!z_{k,l} + \sum_{k=1}^N\sum_{l=1}^Q\dfrac{1}{2}\left(\dfrac{\partial f}{\partial x_{k,l}} + i \dfrac{\partial f}{\partial y_{k,l}}\right)\operatorname{d}\!z^*_{k,l}\end{aligned}$

对比 $\operatorname{d}\!f = \sum\limits_{k=1}^N\sum\limits_{l=1}^Q\dfrac{\partial f}{\partial z_{k,l}} \operatorname{d}\!z_{k,l} + \sum\limits_{k=1}^N\sum\limits_{l=1}^Q \dfrac{\partial f}{\partial z^*_{k,l}} \operatorname{d}\!z^*_{k,l}$ 与上式，可以得到

$\quad\left.\begin{aligned}\dfrac{\partial f}{\partial z_{k,l}} &= \dfrac{1}{2}\left(\dfrac{\partial f}{\partial x_{k,l}} - i \dfrac{\partial f}{\partial y_{k,l}}\right)\\\\\dfrac{\partial f}{\partial z^*_{k,l}}&=\dfrac{1}{2}\left(\dfrac{\partial f}{\partial x_{k,l}} + i \dfrac{\partial f}{\partial y_{k,l}}\right)\end{aligned}\ \right\}$

即定理一的结论也适用于矩阵变量 $\mathbf{Z}$ 和 $\mathbf{Z}^*$。

将上述关系式写成矩阵形式，则有

$\quad\operatorname{d}\!\mathbf{Z} = \operatorname{d}\operatorname{Re}\{\mathbf{Z}\} + i\operatorname{d}\operatorname{Im}\{\mathbf{Z}\} = \operatorname{d}\!\mathbf{X} + i\operatorname{d}\!\mathbf{Y}$
$\quad\operatorname{d}\!\mathbf{Z}^* = \operatorname{d}\operatorname{Re}\{\mathbf{Z}\} - i\operatorname{d}\operatorname{Im}\{\mathbf{Z}\} = \operatorname{d}\!\mathbf{X} - i\operatorname{d}\!\mathbf{Y}$

$\quad\operatorname{d}\operatorname{Re}\{\mathbf{Z}\} = \operatorname{d}\!\mathbf{X} = \frac{1}{2}(\operatorname{d}\!\mathbf{Z} + i\operatorname{d}\!\mathbf{Z}^*)$
$\quad\operatorname{d}\operatorname{Im}\{\mathbf{Z}\} = \operatorname{d}\!\mathbf{Y} = \frac{1}{2}(\operatorname{d}\!\mathbf{Z} - i\operatorname{d}\!\mathbf{Z}^*)$

复微分的基础性质

根据复矩阵微分的定义，容易证明以下结论：

函数 $f$	微分 $\operatorname{d}\!f$
$\mathbf{A}$	$\mathbf{0}$
$a\mathbf{Z}$	$a \operatorname{d}\!\mathbf{Z}$
$\mathbf{A}\mathbf{Z}\mathbf{B}$	$\mathbf{A}(\operatorname{d}\!\mathbf{Z})\mathbf{B}$
$\mathbf{Z}_0 + \mathbf{Z}_1$	$\operatorname{d}\!\mathbf{Z}_0 + \operatorname{d}\!\mathbf{Z}_1$
$\operatorname{Tr}\{\mathbf{Z}\}$	$\operatorname{Tr}\{\operatorname{d}\!\mathbf{Z}\}$
$\mathbf{Z}_0\mathbf{Z}_1$	$(\operatorname{d}\!\mathbf{Z}_0)\mathbf{Z}_1 + \mathbf{Z}_0(\operatorname{d}\!\mathbf{Z}_1)$
$\mathbf{Z}_0 \otimes \mathbf{Z}_1$	$(\operatorname{d}\!\mathbf{Z}_0) \otimes \mathbf{Z}_1 + \mathbf{Z}_0 \otimes (\operatorname{d}\!\mathbf{Z}_1)$
$\mathbf{Z}_0 \odot \mathbf{Z}_1$	$(\operatorname{d}\!\mathbf{Z}_0) \odot \mathbf{Z}_1 + \mathbf{Z}_0 \odot (\operatorname{d}\!\mathbf{Z}_1)$
逐元素函数 $\sigma(\mathbf{Z})$	$\sigma^\prime (\mathbf{Z}) \odot \operatorname{d}\!\mathbf{Z}$
$\mathbf{Z}^{-1}$	$-\mathbf{Z}^{-1} (\operatorname{d}\!\mathbf{Z}) \mathbf{Z}^{-1}$
$\operatorname{det}(\mathbf{Z})$	$\operatorname{det}(\mathbf{Z}) \operatorname{Tr}\{\mathbf{Z}^{-1} \operatorname{d}\!\mathbf{Z}\}\qquad$（如果 $\mathbf{Z}$ 可逆）
$\ln(\operatorname{det}(\mathbf{Z}))$	$\operatorname{Tr}\{\mathbf{Z}^{-1} \operatorname{d}\!\mathbf{Z}\}\qquad$（如果 $\mathbf{Z}$ 可逆）
$\operatorname{reshape}(\mathbf{Z})$	$\operatorname{reshape}(\operatorname{d}\!\mathbf{Z})$
$\mathbf{Z}^*$	$(\operatorname{d}\!\mathbf{Z})^*$
$\mathbf{Z}^\textsf{H}$	$(\operatorname{d}\!\mathbf{Z})^\textsf{H}$
$\mathbf{Z}^\#$	$\operatorname{det}(\mathbf{Z}) \left[\operatorname{Tr}\{\mathbf{Z}^{-1} (\operatorname{d}\!\mathbf{Z})\}\mathbf{Z}^{-1} - \mathbf{Z}^{-1}(\operatorname{d}\!\mathbf{Z}) \mathbf{Z}^{-1}\right]$
$\mathbf{Z}^+$	$\begin{aligned}&-\mathbf{Z}^+ (\operatorname{d}\!\mathbf{Z}) \mathbf{Z}^+ + \mathbf{Z}^+ (\mathbf{Z}^+)^\textsf{H} (\operatorname{d}\!\mathbf{Z}^\textsf{H}) (\mathbf{I}_{N \times N} - \mathbf{Z}\mathbf{Z}^\textsf{H}) \\[5pt]&+ (\mathbf{I}_{Q \times Q} - \mathbf{Z}^+\mathbf{Z}) (\operatorname{d}\!\mathbf{Z}^\textsf{H}) (\mathbf{Z}^+)^\textsf{H} \mathbf{Z}^+\end{aligned}$
$e^z = \exp(z)\qquad$（主分支）	$e^z \operatorname{d}\!z$
$\ln(z)\qquad$（主分支）	$\dfrac{1}{z} \operatorname{d}\!z$

一、常量的微分是零

假设 $\mathbf{A} \in \mathbb{C}^{M \times P}$ 是与 $\mathbf{Z} \in \mathbb{C}^{N \times Q}$ 和 $\mathbf{Z}^*$ 无关的矩阵常量，则有：

$\quad\operatorname{d}\!\mathbf{A} = \mathbf{0}_{M \times P}$

二、线性

假设 $\mathbf{A} \in \mathbb{C}^{M \times N}, \mathbf{B} \in \mathbb{C}^{Q \times P}$ 均和 $\mathbf{Z}, \mathbf{Z}^*$ 无关，则有：

$\quad\operatorname{d}\!(\mathbf{A}\mathbf{Z}\mathbf{B}) = \mathbf{A}(\operatorname{d}\!\mathbf{Z})\mathbf{B}$

假设 $\mathbf{Z}_i \in \mathbb{C}^{N \times Q}$ 是不同的复矩阵变量（$i=\{0,1\}$），则有：

$\quad\operatorname{d}\!(\mathbf{Z}_0 + \mathbf{Z}_1) = \operatorname{d}\!\mathbf{Z}_0 + \operatorname{d}\!\mathbf{Z}_1$

三、迹和微分的交换律

假设 $\mathbf{Z} \in \mathbb{C}^{N \times N}$，即 $\mathbf{Z}$ 是方阵，则有：

$\quad\operatorname{d}\!(\operatorname{Tr}\{\mathbf{Z}\}) = \operatorname{Tr}\{\operatorname{d}\!\mathbf{Z}\}$

四、乘法的微分

假设 $\mathbf{Z_0} \in \mathbb{C}^{M \times N}$ 和 $\mathbf{Z_1} \in \mathbb{C}^{N \times P}$ 是两个矩阵变量，则有

$\quad\operatorname{d}\!(\mathbf{Z}_0\mathbf{Z}_1) = (\operatorname{d}\!\mathbf{Z}_0)\mathbf{Z}_1 + \mathbf{Z}_0(\operatorname{d}\!\mathbf{Z}_1)$

五、外积的微分

假设 $\mathbf{Z_0} \in \mathbb{C}^{N \times Q}$ 和 $\mathbf{Z_1} \in \mathbb{C}^{M \times P}$ 是两个矩阵变量，则有

$\quad\operatorname{d}\!(\mathbf{Z}_0 \otimes \mathbf{Z}_1) = (\operatorname{d}\!\mathbf{Z}_0) \otimes \mathbf{Z}_1 + \mathbf{Z}_0 \otimes (\operatorname{d}\!\mathbf{Z}_1)$

其中 $\otimes$ 表示外积（Kronecker 积），$\mathbf{Z}_0 \otimes \mathbf{Z}_1 \in \mathbb{C}^{NM \times QP}$。

六、逐元素乘积的微分

假设 $\mathbf{Z}_i \in \mathbb{C}^{N \times Q}$ 是不同的复矩阵变量（$i=\{0,1\}$），则有：

$\quad\operatorname{d}\!(\mathbf{Z}_0 \odot \mathbf{Z}_1) = \operatorname{d}\!\mathbf{Z}_0 \odot \mathbf{Z}_1 + \mathbf{Z}_0 \odot \operatorname{d}\!\mathbf{Z}_1$

其中 $\odot$ 表示逐元素乘积（Hadamard 积）。

七、逐元素函数的微分

假设 $\sigma$ 是逐元素函数，即 $\sigma(\mathbf{Z}) = [\sigma(z_{k,l})]$ 是逐元素标量函数运算，则有：

$\quad\operatorname{d}\!(\sigma(\mathbf{Z})) = \sigma^\prime(\mathbf{Z})\operatorname{d}\!\mathbf{Z}$

其中 $\sigma^\prime$ 表示函数 $\sigma$ 的导数。

八、逆矩阵的微分

假设 $\mathbf{Z} \in \mathbb{C}^{N \times N}$ 可逆，则有：

$\quad\operatorname{d}\!\mathbf{Z}^{-1} = -\mathbf{Z}^{-1} (\operatorname{d}\!\mathbf{Z}) \mathbf{Z}^{-1}$

〖展开以查看证明〗

对下列公式求导：

$\quad\mathbf{Z} \mathbf{Z}^{-1} = \mathbf{I}_{N \times N}$

可以得到：

$\quad(\operatorname{d}\!\mathbf{Z}) \mathbf{Z}^{-1} + \mathbf{Z}\operatorname{d}\!\mathbf{Z}^{-1} = \operatorname{d}\!\mathbf{I}_{N \times N} = \mathbf{0}_{N \times N}$

从而可以推出上述等式。

九、reshape 的微分

令 $\operatorname{reshape}$ 是任意一个针对矩阵的线性 reshaping 操作^[11]，则有：

$\quad\operatorname{d}\operatorname{reshape}(\mathbf{Z}) = \operatorname{reshape}(\operatorname{d}\!\mathbf{Z})$

其中 $\operatorname{reshape}$ 具有线性性质：

$\quad\operatorname{reshape}(\mathbf{A} + \mathbf{B}) = \operatorname{reshape}(\mathbf{A}) + \operatorname{reshape}(\mathbf{B})$

十、共轭/共轭转置的微分

$\quad\operatorname{d}\!\mathbf{Z}^* = (\operatorname{d}\!\mathbf{Z})^*$

$\quad\operatorname{d}\!\mathbf{Z}^\textsf{H} = (\operatorname{d}\!\mathbf{Z})^\textsf{H}$

十一、行列式的微分

假设 $\mathbf{Z} \in \mathbb{C}^{N \times N}$，则有：

$\quad\operatorname{d} \operatorname{det}(\mathbf{Z}) = \operatorname{Tr}\{\boldsymbol{C}^\textsf{T}(\mathbf{Z})\ \operatorname{d}\!\mathbf{Z}\}$

其中矩阵 $\boldsymbol{C}(\mathbf{Z}) \in \mathbb{C}^{N \times N}$ 包含 $\mathbf{Z}$ 所有代数余子式 $c_{k,l}(\mathbf{Z})$，即 $(\boldsymbol{C}(\mathbf{Z}))_{k,l} = c_{k,l}(\mathbf{Z})$。

$c_{k,l}(\mathbf{Z}) = (-1)^{k+l} m_{k,l}(\mathbf{Z})$，其中余子式 $m_{k,l}(\mathbf{Z})$ 表示从矩阵 $\mathbf{Z}$ 中删去第 $k$ 行和第 $l$ 列之后得到的 $(N-1) \times (N-1)$ 维子矩阵的行列式。
代数余子式与行列式的关系如下：

$\quad\operatorname{det}(\mathbf{Z}) = \sum\limits_{k=1}^N c_{k,l}(\mathbf{Z}) z_{k,l}$

进一步地，如果 $\mathbf{Z}$ 是可逆矩阵，则有：

$\quad\operatorname{d} \operatorname{det}(\mathbf{Z}) = \operatorname{det}(\mathbf{Z}) \operatorname{Tr}\{\mathbf{Z}^{-1} \operatorname{d}\!\mathbf{Z}\}$

如果矩阵 $\mathbf{Z}$ 可逆，则有以下关系成立：

$\quad\boldsymbol{C}^\textsf{T}(\mathbf{Z}) = \mathbf{Z}^\# = \operatorname{det}(\mathbf{Z}) \mathbf{Z}^{-1}$

其中 $\mathbf{Z}^{\#}$ 是矩阵 $\mathbf{Z}$ 的伴随矩阵，满足 $\mathbf{Z}\mathbf{Z}^\# = \mathbf{Z}^\#\mathbf{Z} = \operatorname{det}(\mathbf{Z})\ \mathbf{I}_{N \times N}$。

由上述关系很容易推出：

$\quad\operatorname{d}\ln(\operatorname{det}(\mathbf{Z})) = \operatorname{Tr}\{\mathbf{Z}^{-1} \operatorname{d}\!\mathbf{Z}\}$

其中对于 $\ln$ 函数我们只采用了它的主分支，并且有 $\operatorname{d}\ln(z) = \dfrac{1}{z} \operatorname{d}\!z$。

十二、Moore-Penrose 广义逆矩阵的微分

假设 $\mathbf{Z}^+ \in \mathbb{C}^{Q \times N}$ 是矩阵 $\mathbf{Z} \in \mathbb{C}^{N \times Q}$ 的 Moore-Penrose 广义逆矩阵，则有：

$\quad\begin{aligned}\operatorname{d}\!\mathbf{Z}^+ =& -\mathbf{Z}^+ (\operatorname{d}\!\mathbf{Z}) \mathbf{Z}^+ + \mathbf{Z}^+ (\mathbf{Z}^+)^\textsf{H} (\operatorname{d}\!\mathbf{Z}^\textsf{H}) (\mathbf{I}_{N \times N} - \mathbf{Z}\mathbf{Z}^\textsf{H}) \\[5pt]&+ (\mathbf{I}_{Q \times Q} - \mathbf{Z}^+\mathbf{Z}) (\operatorname{d}\!\mathbf{Z}^\textsf{H}) (\mathbf{Z}^+)^\textsf{H} \mathbf{Z}^+\end{aligned}$

Moore-Penrose 广义逆矩阵 $\mathbf{Z}^+$ 满足以下性质：

$\quad$任何矩阵 $\mathbf{Z}$ 都存在唯一的 Moore-Penrose 广义逆矩阵 $\mathbf{Z}^+$。

$\quad\mathbf{Z}\mathbf{Z}^+\mathbf{Z} = \mathbf{Z}$

$\quad\mathbf{Z}^+\mathbf{Z}\mathbf{Z}^+ = \mathbf{Z}^+$

$\quad\mathbf{Z}\mathbf{Z}^+$ 和 $\mathbf{Z}^+\mathbf{Z}$ 都是 Hermitian 矩阵。

$\quad$如果 $\mathbf{Z}$ 的所有列向量线性独立，则 $\mathbf{Z}^+ = (\mathbf{Z}^\textsf{H}\mathbf{Z})^{-1} \mathbf{Z}^\textsf{H}$；

$\quad$如果 $\mathbf{Z}$ 的所有行向量线性独立，则 $\mathbf{Z}^+ = \mathbf{Z}^\textsf{H} (\mathbf{Z}\mathbf{Z}^\textsf{H})^{-1}$。

$\quad$如果 $\mathbf{Z}$ 可逆，则 $\mathbf{Z}^+ = \mathbf{Z}^{-1}$。

梯度与微分的关系

[R6] 介绍了标量函数关于实向量 $\boldsymbol{x} \in \mathbb{R}^N$ 的梯度与微分的关系：

$\quad\operatorname{d}\!f = \sum\limits_{k=1}^N \dfrac{\partial f}{\partial x_k} \operatorname{d}\!x_k = \left(\dfrac{\partial f}{\partial \boldsymbol{x}}\right)^\textsf{T} \operatorname{d}\!\boldsymbol{x}$

对关于复向量 $\boldsymbol{z} \in \mathbb{C}^N$ 和 $\boldsymbol{z}^*$ 的标量函数 $f$，我们同样可以得到类似的关系：

$\quad\begin{aligned}\operatorname{d}\!f &= \sum\limits_{k=1}^N \dfrac{\partial f}{\partial z_k} \operatorname{d}\!z_k + \sum\limits_{k=1}^N \dfrac{\partial f}{\partial z^*_k} \operatorname{d}\!z^*_k \\[15pt]&= \left(\dfrac{\partial f}{\partial \boldsymbol{z}}\right)^\textsf{T} \operatorname{d}\!\boldsymbol{z} + \left(\dfrac{\partial f}{\partial \boldsymbol{z}^*}\right)^\textsf{T} \operatorname{d}\!\boldsymbol{z}^*\end{aligned}$

更进一步地，我们也可以将矩阵导数与微分建立联系：

$\quad\begin{aligned}\operatorname{d}\!f &= \sum\limits_{k=1}^N\sum\limits_{l=1}^Q\dfrac{\partial f}{\partial z_{k,l}} \operatorname{d}\!z_{k,l} + \sum\limits_{k=1}^N\sum\limits_{l=1}^Q \dfrac{\partial f}{\partial z^*_{k,l}} \operatorname{d}\!z^*_{k,l}\\[15pt]&= \operatorname{Tr}\left\{\left(\dfrac{\partial f}{\partial \mathbf{Z}}\right)^\textsf{T} \operatorname{d}\!\mathbf{Z}\right\} + \operatorname{Tr}\left\{\left(\dfrac{\partial f}{\partial \mathbf{Z}^*}\right)^\textsf{T} \operatorname{d}\!\mathbf{Z}^*\right\}\end{aligned}$

再结合一些迹技巧（trace trick）：

$\quad$ 标量的迹等于标量本身：$\operatorname{Tr}\{a\} = a$

$\quad$ 转置与迹的关系：$\operatorname{Tr}\{\mathbf{Z}^\textsf{T}\} = \operatorname{Tr}(\mathbf{Z})$，$\operatorname{Tr}\{\mathbf{Z}^\textsf{H}\} = \operatorname{Tr}(\mathbf{Z}^*)$

$\quad$ 矩阵加法与迹的关系：$\operatorname{Tr}\{\mathbf{Z}_0 \pm \mathbf{Z}_1\} = \operatorname{Tr}\{\mathbf{Z}_0\} \pm \operatorname{Tr}\{\mathbf{Z}_1\}$

$\quad$ 矩阵乘法与迹的关系：$\operatorname{Tr}\{\mathbf{Z}_0 \mathbf{Z}_1\} = \operatorname{Tr}\{\mathbf{Z}_1 \mathbf{Z}_0\}$

$\quad$ 矩阵乘法、逐元素乘法与迹的关系：$\operatorname{Tr}\{\mathbf{Z}_0^\textsf{T} (\mathbf{Z}_1 \odot \mathbf{Z}_2)\} = \operatorname{Tr}\{(\mathbf{Z}_0 \odot \mathbf{Z}_1)^\textsf{T} \mathbf{Z}_2\} = \sum\limits_{k,l}z_{0,k,l}z_{1,k,l}z_{2,k,l}$

就很容易推导出常见函数关于矩阵 $\mathbf{Z}$ 或向量 $\boldsymbol{z}$ 的偏导数了。

---

梯度与微分关系的应用实例

实例一

假设 $\boldsymbol{a} \in \mathbb{C}^{1 \times N}$ 和 $\boldsymbol{b} \in \mathbb{C}^{Q \times 1}$ 是与变量 $\mathbf{Z} \in \mathbb{C}^{N \times Q}$ 和 $\mathbf{Z}^*$ 无关的向量常量，对于标量函数 $f(\mathbf{Z}) = \boldsymbol{a}^\textsf{T}\mathbf{Z}\boldsymbol{b}$，求证 $\dfrac{\partial f}{\mathbf{Z}} = \boldsymbol{a}\boldsymbol{b}^\textsf{T}$。

解： 先利用矩阵乘法与微分的关系以及迹技巧，可以得到：

$\quad\begin{aligned}\operatorname{d}\!f &= \cancel{(\operatorname{d} \!\boldsymbol{a}^\textsf{T})\mathbf{Z}\boldsymbol{b}} + \boldsymbol{a}^\textsf{T}(\operatorname{d}\!\mathbf{Z})\boldsymbol{b} + \cancel{\boldsymbol{a}^\textsf{T}\mathbf{Z}(\operatorname{d}\!\boldsymbol{b})} \\[5pt]&= \boldsymbol{a}^\textsf{T}(\operatorname{d}\!\mathbf{Z})\boldsymbol{b} \\[5pt]&= \operatorname{Tr}\{\boldsymbol{a}^\textsf{T}(\operatorname{d}\!\mathbf{Z})\boldsymbol{b}\} = \operatorname{Tr}\{\boldsymbol{b}\boldsymbol{a}^\textsf{T}(\operatorname{d}\!\mathbf{Z})\} = \operatorname{Tr}\left\{\left(\boldsymbol{a}\boldsymbol{b}^\textsf{T}\right)^\textsf{T} \operatorname{d}\!\mathbf{Z}\right\}\end{aligned}$

又根据梯度与微分的关系，我们有 $\operatorname{d}\!f = \operatorname{Tr}\left\{\left(\dfrac{\partial f}{\partial \mathbf{Z}}\right)^\textsf{T} \operatorname{d}\!\mathbf{Z}\right\} + \operatorname{Tr}\left\{\left(\dfrac{\partial f}{\partial \mathbf{Z}^*}\right)^\textsf{T} \operatorname{d}\!\mathbf{Z}^*\right\}$

比较上面两个公式的对应项，即可得到：

$\quad\left.\begin{aligned}\dfrac{\partial f}{\partial \mathbf{Z}} &= \boldsymbol{a}\boldsymbol{b}^\textsf{T}\\\\\dfrac{\partial f}{\partial \mathbf{Z}^*} &= \mathbf{0}\end{aligned}\ \right\}$

实例二

假设 $\mathbf{Z} \in \mathbb{C}^{N \times Q}$ 和 $\boldsymbol{y} \in \mathbb{C}^{N \times 1}$ 是与向量 $\boldsymbol{w} \in \mathbb{C}^{Q \times 1}$ 和 $\boldsymbol{w}^*$ 无关的常量，对于关于 $\boldsymbol{w}$ 的标量函数 $f(\boldsymbol{w}) = \|\mathbf{Z}\boldsymbol{w} - \boldsymbol{y}\|^2$，求证函数 $f$ 的零点是 $\boldsymbol{w} = (\mathbf{Z}^\textsf{H}\mathbf{Z})^{-1} \mathbf{Z}^\textsf{H} \boldsymbol{y}$。

解： 先将函数改写成向量内积的形式并化简：$f(\boldsymbol{w}) = (\mathbf{Z}\boldsymbol{w} - \boldsymbol{y})^\textsf{H} (\mathbf{Z}\boldsymbol{w} - \boldsymbol{y})$

然后利用矩阵/向量乘法与微分的关系以及迹技巧，可以得到：

$\quad\begin{aligned}\operatorname{d}\!f &= (\mathbf{Z}\operatorname{d}\!\boldsymbol{w})^\textsf{H} (\mathbf{Z}\boldsymbol{w} - \boldsymbol{y}) + (\mathbf{Z}\boldsymbol{w} - \boldsymbol{y})^\textsf{H} (\mathbf{Z}\operatorname{d}\!\boldsymbol{w}) \\[5pt]&= (\operatorname{d}\!\boldsymbol{w})^\textsf{H}\mathbf{Z}^\textsf{H}(\mathbf{Z}\boldsymbol{w} - \boldsymbol{y}) + (\boldsymbol{w}^\textsf{H}\mathbf{Z}^H - \boldsymbol{y}^\textsf{H}) \mathbf{Z} \operatorname{d}\!\boldsymbol{w} \\[5pt]&= \operatorname{Tr}\left\{(\operatorname{d}\!\boldsymbol{w})^\textsf{H}\mathbf{Z}^\textsf{H}(\mathbf{Z}\boldsymbol{w} - \boldsymbol{y})\right\} + \operatorname{Tr}\left\{(\boldsymbol{w}^\textsf{H}\mathbf{Z}^H - \boldsymbol{y}^\textsf{H}) \mathbf{Z} \operatorname{d}\!\boldsymbol{w}\right\} \\[5pt]&= \operatorname{Tr}\left\{(\mathbf{Z}\boldsymbol{w} - \boldsymbol{y})^\textsf{T} \mathbf{Z}^*(\operatorname{d}\!\boldsymbol{w}^*)\right\} + \operatorname{Tr}\left\{\left(\mathbf{Z}^\textsf{T} (\mathbf{Z}^*\boldsymbol{w}^* - \boldsymbol{y}^*)\right)^\textsf{T} \operatorname{d}\!\boldsymbol{w}\right\} \\[5pt]&= \operatorname{Tr}\left\{\left(\mathbf{Z}^\textsf{H} (\mathbf{Z}\boldsymbol{w} - \boldsymbol{y})\right)^\textsf{T} \operatorname{d}\!\boldsymbol{w}^*\right\} + \operatorname{Tr}\left\{\left(\mathbf{Z}^\textsf{T} (\mathbf{Z}^*\boldsymbol{w}^* - \boldsymbol{y}^*)\right)^\textsf{T} \operatorname{d}\!\boldsymbol{w}\right\}\end{aligned}$

又根据梯度与微分的关系，我们有 $\operatorname{d}\!f = \operatorname{Tr}\left\{\left(\dfrac{\partial f}{\partial \boldsymbol{w}}\right)^\textsf{T} \operatorname{d}\!\boldsymbol{w}\right\} + \operatorname{Tr}\left\{\left(\dfrac{\partial f}{\partial \boldsymbol{w}^*}\right)^\textsf{T} \operatorname{d}\!\boldsymbol{w}^*\right\}$

比较上面两个公式的对应项，即可得到：

$\quad\left.\begin{aligned}\dfrac{\partial f}{\partial \boldsymbol{w}} &= \mathbf{Z}^\textsf{T} (\mathbf{Z}^*\boldsymbol{w}^* - \boldsymbol{y}^*)\\\\\dfrac{\partial f}{\partial \boldsymbol{w}^*} &= \mathbf{Z}^\textsf{H} (\mathbf{Z} \boldsymbol{w} - \boldsymbol{y})\end{aligned}\ \right\}$

令 $\dfrac{\partial f}{\partial \boldsymbol{w}}$ 和 $\dfrac{\partial f}{\partial \boldsymbol{w}^*}$ 中的任意一个等于零，即可得到 $\boldsymbol{w}$ 的最小二乘估计为：

$\quad\boldsymbol{w} = (\mathbf{Z}^\textsf{H}\mathbf{Z})^{-1} \mathbf{Z}^\textsf{H} \boldsymbol{y}$

参考文献

[R1] D. Brandwood, “A complex gradient operator and its application in adaptive array theory,” IEE Proceedings H (Microwaves, Optics and Antennas), vol. 130, pp. 11–16, 1983.

[R2] “Wirtinger derivatives,” Wikipedia. https://en.wikipedia.org/wiki/Wirtinger_derivatives

[R3] A. Hjørungnes, “Complex-valued matrix derivatives: With applications in signal processing and communications,” Cambridge University Press, 2011.

[R4] Kaare Brandt Petersen and Michael Syskind Pedersen, “The matrix cookbook,” Technical University of Denmark, 2012, Nov.

[R5] “Matrix calculus,” Wikipedia. https://en.wikipedia.org/wiki/Matrix_calculus

[R6] 长躯鬼侠, “矩阵求导术（上）,” 知乎, 2020. https://zhuanlan.zhihu.com/p/24709748

[R7] 长躯鬼侠, “矩阵求导术（下）,” 知乎, 2020. https://zhuanlan.zhihu.com/p/24863977

[R8] B. Widrow, J. McCool, and M. Ball, “The complex LMS algorithm,” Proceedings of the IEEE, vol. 63, no. 4, pp. 719–720, 1975.

---

1. 一个函数是解析的（analytic），当且仅当它在定义域内的每个点的邻域内的 Tayler 级数都收敛。 ↩︎

2. 所有的复解析函数都是全纯函数（holomorphic function），反之亦然。全纯函数是指满足在其定义域内的每个点的邻域内处处复可微的单复变函数或多复变函数。 ↩︎

3. 常见的复解析函数有：所有关于 $z$ 的复系数多项式函数、$\exp(z)$、三角函数、双曲函数 $\sinh z = \frac{\exp(z) - \exp(-z)}{2}$ 和 $\cosh z = \frac{\exp(z) + \exp(-z)}{2}$。此外，对数函数 $\log z$ 的主分支在域 $\mathbb{C} \setminus \{z\in\mathbb{R}: z \le 0\}$ 上全纯，根式函数 如平方根函数 $\sqrt{z} = \exp(\frac{1}{2} \log z)$ 因此也在 $\log z$ 全纯时为全纯函数；倒数 $1/z$ 在域 $\mathbb{C} \setminus \{0\}$ 上全纯，更一般地，$z$ 的有理式函数在除去其分母的零点外的整个复数域上全纯。 ↩︎

4. 常见的不是复解析函数的例子：取模 $|z|$、取辐角 $\arg(z)$、复共轭 $z^*$、取实部 $\operatorname{Re}\{z\}$、取虚部 $\operatorname{Im}\{z\}$。 ↩︎

5. 推荐阅读：http://jiaxuanli.me/blog/2017/12/数学物理方法 中的 第二章：解析函数 ↩︎

6. 原文中是 analytic restricted function，此处不知如何翻译比较好。 ↩︎

7. Cauchy-Riemann 条件构成一个复变函数是解析函数的充分必要条件。 ↩︎

8. 信号处理中很多情况会出现这种形式的函数，如（窄带）自适应阵列理论中常见的输出功率 $\mathbf{w}^\textsf{H}\mathbf{\Phi}\mathbf{w}$ 可以看作关于复向量 $\mathbf{w}$ 的实值函数。 ↩︎

9. 参考 https://en.wikipedia.org/wiki/Inner_product_space ↩︎

10. 详情请参考 https://en.wikipedia.org/wiki/Function_composition ↩︎

11. 线性 reshaping 操作可以删除输入矩阵中的特定元素、保留所有输入元素、复制多份特定输入元素等。 ↩︎